Fourier domain least squares engine. More...
#include <stfinvfdleastsquares.h>
Public Types | |
| typedef Tfftengine::TAseries | TAseries |
| type of array for time series values More... | |
| typedef Tfftengine::TAspectrum | TAspectrum |
| type of array for Fourier transforms More... | |
| typedef stfinv::STFFourierDomainEngine | Tbase |
| typedef to refer to base class More... | |
| typedef fourier::fft::DRFFTWAFFArrayEngine | Tfftengine |
| type of underlying Fourier engine More... | |
Public Member Functions | |
| STFEngineFDLeastSquares (const stfinv::Tvectoroftriples &triples, const stfinv::Waveform &stf, const std::string ¶meters) | |
| Constructor. More... | |
| STFEngineFDLeastSquares (const stfinv::Tvectoroftriples &triples, const stfinv::Waveform &stf, const stfinv::Tvectorofpairs &pairs, const std::string ¶meters) | |
| Constructor. More... | |
| virtual | ~STFEngineFDLeastSquares () |
| abstract base requires virtual destructor More... | |
| virtual void | exec () |
| Start engine. More... | |
| virtual void | help (std::ostream &os=std::cout) const |
| print online help More... | |
| virtual const char * | name () const |
| return name of engine More... | |
| virtual void | usage (std::ostream &os=std::cout) const |
| print detailed description More... | |
Basic interface for users | |
| stfinv::Waveform | run () |
| Start engine and return reference to source correction filter. More... | |
Shape query functions | |
| unsigned int | nsamples () const |
| return number of samples used in time series More... | |
| unsigned int | nreceivers () const |
| return number of receiver signals in use More... | |
| unsigned int | npairs () const |
| return number of additional signals to be convolved More... | |
| double | dt () const |
| return sampling interval More... | |
Data query functions | |
| Tseries | stf () const |
| return source correction filter series More... | |
| Tseries::Tcoc | recording (const unsigned int &i) const |
return recorded data at receiver i More... | |
| Tseries::Tcoc | synthetic (const unsigned int &i) const |
return synthetic data at receiver i More... | |
| Tseries | convolvedsynthetic (const unsigned int &i) const |
return synthetic data convolved with stf at receiver i More... | |
| Tseries::Tcoc | series (const unsigned int &i) const |
return synthetic data of pair i More... | |
| Tseries | convolvedseries (const unsigned int &i) const |
return synthetic data convolved with stf for pair i More... | |
Static Public Member Functions | |
| static void | classhelp (std::ostream &os=std::cout) |
| print online help More... | |
| static void | classusage (std::ostream &os=std::cout) |
| print detailed description More... | |
Static Public Attributes | |
| static const char *const | description ="least squares in the frequency domain" |
| short description of this engine More... | |
| static const char *const | ID ="fdlsq" |
| ID used to select this engine. More... | |
Protected Member Functions | |
Access and control functions to be used by derived classes. | |
These functions are part of the interface implemented in STFFourierDomainEngine. | |
| void | fftinput () |
| copy input signals to workspace and transform input workspace to Fourier domain More... | |
| void | fftoutput () |
| convolve synthetics with Fourier transform of stf and transform convolved synthetics and stf to time domain and pass signals to user memory space More... | |
| TAspectrum | recordingspec () const |
| return reference to Fourier transform of recorded data More... | |
| TAspectrum | syntheticspec () const |
| return reference to Fourier transform of synthetics More... | |
| TAspectrum | stfspec () const |
| return reference to Fourier transform of stf More... | |
| TAspectrum | recordingcoeff (const unsigned int &i) const |
| return reference to Fourier coeffients of recorded data for frequency i More... | |
| TAspectrum | syntheticcoeff (const unsigned int &i) const |
| return reference to Fourier coefficients of synthetics for frequency i More... | |
| TAspectrum::Tvalue & | stfcoeff (const unsigned int &i) const |
| return reference to Fourier coefficients of stf for frequency i More... | |
| double | frequency (const unsigned int &i) const |
| return value of frequency i in Hz More... | |
| unsigned int | nfreq () const |
| return number of frequencies in use More... | |
Functions presented to derived classes | |
| std::string | parameter (const std::string &key, const std::string &defvalue="false") const |
| return the value of a parameters More... | |
| bool | parameterisset (const std::string &key) const |
| check is parameter was set by user More... | |
| void | checkreceiverindex (const unsigned int &i) const |
| check for vaid receiver index More... | |
| void | checkseriesindex (const unsigned int &i) const |
| check for vaid index off additional time series pair More... | |
| double | weight (const unsigned int &i) const |
| return weight for signal at receiver i More... | |
| aff::Series< double > | weights () const |
| return weights array More... | |
Protected Attributes | |
| int | Mdebug |
| debug level More... | |
| stfinv::Tvectorofpairs | Mpairs |
| Waveform pairs. More... | |
| stfinv::Waveform | Mstf |
| source correction filter. More... | |
| stfinv::Tvectoroftriples | Mtriples |
| Waveform triples. More... | |
| int | Mverbose |
| verbose level More... | |
Private Member Functions | |
| void | initialize () |
| initialize work space More... | |
Private Attributes | |
| double | Mwaterlevel |
| waterlevel More... | |
Detailed Description
Fourier domain least squares engine.
- Concept behind this engine
- If
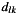 is the Fourier coefficient of recorded data at Frequency
is the Fourier coefficient of recorded data at Frequency 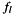 and receiver
and receiver 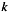 at offset
at offset 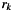 ,
,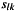 is the Fourier coefficient of the corresponding synthetics and
is the Fourier coefficient of the corresponding synthetics and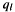 is that of the sought source tim function,
is that of the sought source tim function,
with respect to the real part![\[ E=\sum\limits_{l,k}\left|w_{lk}\, \left(d_{lk}-s_{lk}q_l\right) \right|^2+\sum\limits_{l}\lambda^2\left|q_l\right|^2 =\chi^2+\psi^2 \]](form_6.png)
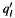 and the imaginary part
and the imaginary part 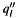 of
of
In the above expression![\[ q_l=q_l^\prime+i\,q_l^{\prime\prime}. \]](form_9.png)
is the data misfit with weights![\[ \chi^2=\sum\limits_{l,k}\left|w_{lk}\, \left(d_{lk}-s_{lk}q_l\right) \right|^2 \]](form_10.png)
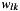 and
and
is used for regularization and will introduce a water-level in the deconvolution.![\[ \psi^2=\sum\limits_{l}\lambda^2\left|q_l\right|^2 \]](form_12.png)
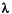 will balance both contributions. The conditions
will balance both contributions. The conditions
result in (Forbriger, 2001, appendix A.3)![\[ \frac{\partial E}{\partial q_l^\prime}\stackrel{!}{=}0 \quad\wedge\quad \frac{\partial E}{\partial q_l^{\prime\prime}}\stackrel{!}{=}0 \]](form_14.png)
where![\[ q_l=\frac{ \eta^2\sum\limits_{k}f_k^2\,s_{kl}^\ast\,d_{kl} }{ \lambda^2+\eta^2\sum\limits_{k}f_k^2\,s_{kl}^\ast\,s_{kl} } \quad\forall\, l \]](form_15.png)
and![\[ w_{lk}=\eta\,f_k \]](form_16.png)
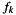 is a receiver specific weighting factor. Now
is a receiver specific weighting factor. Now 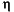 and
and 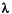 have to be used to balance the regularization. We aim to specify a waterlevel as a fraction of synthetic data energy.
have to be used to balance the regularization. We aim to specify a waterlevel as a fraction of synthetic data energy.
- Setting up the waterlevel
- The misfit equals one if the scaled energy of the residual
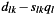 equals the scaled energy of the synthetics
equals the scaled energy of the synthetics 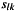 and
and
is the reciprocal of the scaled energy of the synthetics. If we then choose![\[ \eta^2=\frac{1}{\sum\limits_k f_k^2\sum\limits_l \left|s_{lk}\right|^2} \]](form_20.png)
where![\[ \frac{\lambda^2}{\eta^2}=\frac{\epsilon^2}{N\eta^2}= \frac{\epsilon^2}{N}\sum\limits_k f_k^2\sum\limits_{l=0}^{N-1} \left|s_{lk}\right|^2 \]](form_21.png)
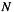 is the number of frequencies, then
is the number of frequencies, then 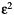 will specify a waterlevel as a fraction of the scaled energy of the synthetics.
will specify a waterlevel as a fraction of the scaled energy of the synthetics.
- Using Parceval's Theorem to calculate signal energy
- Parceval's Theorem for a signal
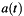 and its Fourier transform
and its Fourier transform 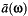 is
is
If![\[ \int\limits_{-\infty}^{+\infty}\bigl|a(t)\bigr|^2\,\textrm{d} t= \int\limits_{-\infty}^{+\infty}\bigl|\tilde{a}(\omega)\bigr|^2\, \frac{\textrm{d} \omega}{2\pi}. \]](form_26.png)
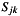 are the time series samples corresponding to the Fourier coefficients
are the time series samples corresponding to the Fourier coefficients 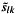 and
and 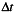 is the sampling interval then
is the sampling interval then
where![\[ \sum\limits_{k=0}^{M-1}\left|S_{jk}\right|^2\,\Delta t= \sum\limits_{l=0}^{M-1}\left|\tilde{s}_{lk}\right|^2\,\frac{1}{M\,\Delta t}, \]](form_30.png)
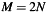 is the number of samples in the time series. In the above calculation the energy sum only uses the positive frequencies and
is the number of samples in the time series. In the above calculation the energy sum only uses the positive frequencies and
Fourier coefficients![\[ \sum\limits_k f_k^2\sum\limits_{l=0}^{N-1}\left|\tilde{s}_{lk}\right|^2 = N\,(\Delta t)^2\, \sum\limits_k f_k^2 \sum\limits_{j=0}^{2N-1}\left|S_{jk}\right|^2. \]](form_32.png)
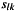 calculated by the stfinv::STFFourierDomainEngine are not scaled (see documentation of libfourierxx and libfftw3), such that
calculated by the stfinv::STFFourierDomainEngine are not scaled (see documentation of libfourierxx and libfftw3), such that
(both,![\[ \Delta t\,s_{lk}=\tilde{s}_{lk} \]](form_33.png)
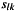 and
and 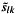 are Fourier coefficients). Consequently
are Fourier coefficients). Consequently ![\[ \sum\limits_k f_k^2\sum\limits_{l=0}^{N-1}\left|s_{lk}\right|^2 = N\, \sum\limits_k f_k^2 \sum\limits_{j=0}^{2N-1}\left|S_{jk}\right|^2. \]](form_34.png)
- Final calculation recipe
- The solution to our problem is
where![\[ q_l=\frac{ \sum\limits_{k}f_k^2\,s_{lk}^\ast\,d_{lk} }{ \epsilon^2\,\sum\limits_k f_k^2 \sum\limits_{j=0}^{2N-1}\left|S_{jk}\right|^2 +\sum\limits_{k}f_k^2\,s_{lk}^\ast\,s_{lk} } \quad\forall\, l, \]](form_35.png)
is the sum of the squared sample values![\[ \sum\limits_{j=0}^{2N-1}\left|S_{jk}\right|^2 \]](form_36.png)
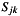 of the synthetic time series for receiver
of the synthetic time series for receiver 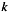 ,
, 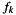 are the scaling factors provided by stfinv::STFBaseEngine::weight(), and
are the scaling factors provided by stfinv::STFBaseEngine::weight(), and 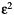 is the water level parameter passed to STFEngineFDLeastSquares.
is the water level parameter passed to STFEngineFDLeastSquares.
- References
- Forbriger, T., 2001. Inversion flachseismischer Wellenfeldspektern. PhD thesis, University of Stuttgart. http://elib.uni-stuttgart.de/opus/volltexte/2001/861/
- Why was it renamed?
- This engine was called 'blind deconvolution' engine. It was renamed to fourier domain least squares engine in October 2011.
This engine understands the recorded data as being the synthetic data being convoled with the STF (source correction filter) and having some noise added. The true impulse response of the subsurface could be obtained by deconvolution of the recorded data with the STF. Neither the impulse response of the subsurface nor the STF are known. For this reason the STF has to be found by minimizing an objective function. For this reason the it is called 'blind' deconvolution.
However, the approach of libstfinv is to convolved the synthetics with the STF to reducde the misfit to the recorded data, not to deconvolve the recorded data. For this reason, maybe, we should better call the approach 'blind convolution'. With respect to image processing techniques, all engines in libstfinv do some kind of 'blind convolution', not only the blind deconvolution engine. Consequently this engine should better be called 'least-squares engine'.
Definition at line 219 of file stfinvfdleastsquares.h.
The documentation for this class was generated from the following files:
