Sections in this page:

One-sided PSD

Power spectral density computed by this program is the so-called one-sided PSD. This is, if P(f) is the Fourier transform of the normalized auto-correlation function, the output of the program is 2P(f). The rms-amplitude in a frequency band (f2-f1) is A=sqrt(2*P(f)*(f2-f1)) if P(f) is constant in the interval (f1,f2).

Scaling of Fourier transforms

The Fourier transform presented in libfourier is scaled appropriately to represent coefficients of the Fourier integral transform (see libfourier documentation).

The maximum of the transform of the Boxcar taper is T, where T is the duration of the window. Similarly the maximum of the Fourier transform of the Hanning taper is 0.5*T, where the duration of the window is T.

Date: 12/2010

Author: thof

Scaling factor for Hanning taper when applied in PSD calculation

Tapering stationary noise with a Hanning taper reduces total signal energy an thus the signal power obtained through an FFT. In his tutorial Agnew recommends to scale each sample 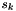$s_k$ of the series by 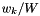$w_k/W$ , where 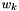$w_k$ is the 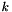$k$ -th sample of the taper and

$W^2 = \frac{1}{N} \sum\limits_0^{N-1} w_k^2$

is a measure for the loss in total signal power due to application of the taper. This applies only for staionary noise.

From Walter's Matlab scripts I took:

If data is the time series vector and y is the Hanning taper of appropriate length, Walter calculates

w = sqrt(sum(y.*y)/ndata);

and

y=y/w;

where ndata is the length of data and y.

For a Hanning taper

$w_k = \sin^2(k \pi/(N-1)).$

Thus

$W^2 = \frac{1}{N} \sum\limits_0^{N-1} \sin^4(k\pi/(N-1))$

From Gradshteyn and Ryzhik (eq. 1.321 3) I find

$\sin^4(k\pi/(N-1)) = \frac{1}{8} \left( \cos(4 k\pi/(N-1)) - 4 \cos(2 k\pi/(N-1)) + 3 \right).$

Within the sum the contribution of both cos-terms will vanish, since both are averaged over one and two periods, respectively. Thus

$W^2 = \frac{1}{N} \sum\limits_0^{N-1} \frac{3}{8} = \frac{3}{8}.$

Since foutra is not scaling the taper but scaling the power spectrum, we have to apply the factor 8/3 to the result of power spectrum calculation.

This factor 8/3=2.66667 was tested against the value for 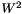$W^2$ , when explicitely derived from a Hanning taper time series by the above formula.

In the Makefile you will find a section with test code. This offers instantaneous testing of PSD scaling in foutra.

Date: 13/9/2007

Author: thof

Scaling for harmonic signals

For harmonic signals the FFT normalized to the duration of the available time window has an amplitude of the value of the maximum of the Fourier transform of the window function times half the amplitude of the time domain signal. To obtain a spectral representation with peaks of the amplitude of the time domain signal, the FFT must be scaled accordingly.

We understand

$\tilde{f}(\omega)=\int\limits_{-\infty}^{+\infty} f(t) \,e^{-i\omega t} \textrm{d}{t}.$

as the Fourier transformation of the time domain signal

$f(t)=\int\limits_{-\infty}^{+\infty} \tilde{f}(\omega) \,e^{i\omega t} \frac{\textrm{d}{\omega}}{2\pi}.$

If we apply a time domain window function 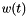$w(t)$ to the function 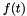$f(t)$ , we obtain the tapered function

$g(t)=f(t) w(t)$

and its Fourier transform

$\tilde{g}(\omega)=\int\limits_{-\infty}^{+\infty} \tilde{f}(\omega')\,\tilde{w}(\omega-\omega')\,\textrm{d}\omega.$

Application to harmonic signals

Let

$f(t)=A\,\cos(\omega_0 t+\phi)$

be the harmonic signal under investigation. Then

$f(t)=A\left\{\cos(\omega_0 t)\cos(\phi)- \sin(\omega_0 t)\sin(\phi)\right\}$

and

$\tilde{f}(\omega) = \frac{A}{2}\left\{ \cos(\phi) \left[ \delta(\omega-\omega_0) + \delta(\omega+\omega_0) \right] +i\sin(\phi) \left[ \delta(\omega-\omega_0) - \delta(\omega+\omega_0) \right] \right\},$

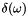where $\delta(\omega)$ is Dirac's delta function with

$\delta(\omega)=\left\{ \begin{array}{ll} \infty & \textrm{if $\omega=0$ and}\\ 0 & \textrm{otherwise} \end{array} \right.$

and

$\int\limits_{-\infty}^{+\infty} \delta(\omega)\,\textrm{d}\omega=1$

such that

$\tilde{f}(\omega)=\int\limits_{-\infty}^{+\infty} \tilde{f}(\omega')\,\delta(\omega-\omega')\,\textrm{d}\omega.$

This way I obtain

$\tilde{g}(\omega)= \frac{A}{2}\left\{ e^{i\phi}\tilde{w}(\omega-\omega_0) + e^{-i\phi}\tilde{w}(\omega+\omega_0) \right\}$

for the Fourier transform of the tapered function. If we ignore interference with side-lobes from the negative frequency 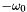$-\omega_0$ and side-lobes of potential other harmonics at nearby frequencies, we can approximate

$\tilde{g}(\omega_0)\approx\frac{A}{2}e^{i\phi}\tilde{w}(0)$

and

$\left|\tilde{g}(\omega_0)\right|\approx \frac{A}{2}\left|\tilde{w}(0)\right|.$

Boxcar taper function

The boxcar taper is defined as

$w(t) = \left\{ \begin{array}{ll} 1 & \textrm{if $|t|\leq T/2$ and}\\ 0 & \textrm{otherwise} \end{array} \right.$

with

$\tilde{w}(\omega) = T \frac{\sin(\omega T/2)}{\omega T/2}$

and

$w_{\textrm{max}}=w(0)=T.$

Hanning taper function

The Hanning taper is defined as

$w(t) = \left\{ \begin{array}{ll} \cos^2(\pi t / T)) = \frac{1}{2}\left[ 1 + \cos(2\pi t / T) \right] & \textrm{if $|t|\leq T/2$ and}\\ 0 & \textrm{otherwise} \end{array} \right.$

with

$\tilde{w}(\omega) = T/2 \frac{\sin(\omega T/2)}{\omega T/2} + T/4 \frac{\sin(\omega T/2+\pi)}{\omega T/2+\pi} + T/4 \frac{\sin(\omega T/2-\pi)}{\omega T/2-\pi}$

(see Blackman, R.B. and Tukey, J.W. 1958. The measurement of power spectra. Dover Publications, Inc., New York. Section B.5) and

$w_{\textrm{max}}=w(0)=\frac{T}{2}.$

Instant tests

In the Makefile you will find a section with test code. This offers instantaneous testing of harmonic signal scaling in foutra.

Date: 10.01.2011

Author: thof