◆ convolve()

template<class T >

aff::Series<T> ts::convolve	(	const aff::ConstSeries< T > &	a,
		const aff::ConstSeries< T > &	b
	)

Calculate convolution of two series.

The function evaluates

$c_k = \sum\limits_l a_l b_{k-l},$

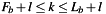where the index ranges of the input series are $a_l: l \in [F_a,L_a]$ and $b_l: l \in [F_b,L_b].$ From the second factor we conclude $F_b +l \leq k \leq L_b + l$ and thus the index range of 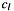$ c_l $ is

$F_b + F_a \leq k \leq L_b + L_a.$

For a given 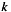$ k $ the range of summation index 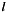$ l $ is defined by the two conditions

$k- L_b \leq l \leq k- F_b$

and

$F_a \leq k \leq L_a.$

Note

This function is designed to be used as a discrete approximation to the convolution integral, if convolved series are sampled versions of functions. This has two consequences:

The result should be appropriately scaled with the sampling interval. The sampling interval is not available to this function. The scaling therefore has to take place in the calling program.
The time series are understood to have infinite length, while all samples outside the provided index range implicitely equal zero. The convolution result then necessarily equals zero for index values 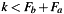and 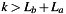. The result 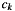will be output for $k \in [F_a+F_b,L_a+L_b]$ with 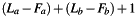samples, thus being longer than either one of the input series. If the convolution filter response is not given completely, but just as a cut-out of the filter response function, the convolution potentially produces a step-response at the end of the filter sequence. This exactly is the behaviour of the convolution integral, if only a cut-out of the originally infinite filter impulse response function is used. If this is missed, the user might be surprised by an unexpected coda in the result of this function. Consider to trim the output sequence to a reasonable sample window to represent a proper cut-out of the expected result.

Parameters

a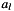
b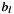

Returns: c

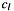
Definition at line 103 of file convolve.h.

Referenced by main().

     {
       aff::Series<T> retval(a.first()+b.first(),b.last()+a.last());
       for (long int k=retval.first(); k<=retval.last(); ++k)
       {
         retval(k)=T(0);
         long int lmin=a.first() > (k-b.last()) ? a.first() : (k-b.last());
         long int lmax=a.last() < (k-b.first()) ? a.last() : (k-b.first());
         for(long int l=lmin; l<=lmax; ++l)
         {
           retval(k)+=a(l)*b(k-l);
         }
       }
       return(retval);
     } // convolve

Here is the caller graph for this function: