◆ correlate()

template<class T >

aff::Series<T> ts::correlate	(	const aff::ConstSeries< T > &	a,
		const aff::ConstSeries< T > &	b
	)

Calculate crosscorrelation of two series.

The function evaluates

$c_k = \sum\limits_l a_l b_{k+l},$

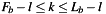where the index ranges of the input series are $a_l: l \in [F_a,L_a]$ and $b_l: l \in [F_b,L_b].$ From the second factor we conclude $F_b -l \leq k \leq L_b - l$ and thus the index range of 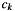$ c_k $ is

$F_b - L_a \leq k \leq L_b - F_a.$

For a given 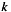$ k $ the range of summation index 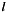$ l $ is defined by the two conditions

$F_b - k \leq l \leq L_b - k$

and

$F_a \leq k \leq L_a.$

Parameters

a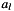
b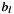

Returns: c

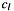
Definition at line 75 of file correlate.h.

     {
       aff::Series<T> retval(b.first()-a.last(),b.last()-a.first());
       for (long int k=retval.first(); k<=retval.last(); ++k)
       {
         retval(k)=T(0);
         long int lmin=a.first() > (b.first()-k) ? a.first() : (b.first()-k);
         long int lmax=a.last() < (b.last()-k) ? a.last() : (b.last()-k);
         for(long int l=lmin; l<=lmax; ++l)
         {
           retval(k)+=a(l)*b(l+k);
         }
       }
       return(retval);
     } // correlate