◆ psdnorm()

double ts::tapers::Hanning::psdnorm ( ) const

privatevirtual

PSD scaling factor

Scaling factor for Hanning taper

Tapering stationary noise with a Hanning taper reduces total signal energy an thus the signal power obtained through an FFT. In his tutorial Agnew recommends to scale each sample 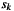$s_k$ of the series by 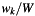$w_k/W$ , where 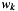$w_k$ is the k-th sample of the taper and

$W^2 = (sum_0^{N-1} w_k ^2) /N$

is a measure for the loss in total signal power due to application of the taper. This applies only for staionary noise.

From Walter's Matlab scripts I took:

If data is the time series vector and y is the Hanning taper of appropriate length, Walter calculates

$w = sqrt(sum(y.*y)/ndata);$

and

$y=y/w;$

where ndata is the length of data and y.

For a Hanning taper:

$w_k = sin^2(k*pi/(N-1))$

Thus

$W^2 = (sum_0^{N-1} sin^4(k*pi/(N-1))) /N$

From Gradshteyn and Ryzhik (eq. 1.321 3) I find

$sin^4(k*pi/(N-1))) = (1/8) * ( cos(4 * k*pi/(N-1)) - 4 * cos(2 * k*pi/(N-1)) + 3 ).$

Within the sum the contribution of both cos-terms will vanish, since both are averaged over one and two periods, respectively. Thus

$W^2 = (sum_0^{N-1} 3/8) /N = 3/8.$

Since foutra is not scaling the taper but scaling the power spectrum, we have to apply the factor 8/3 to the result of power spectrum calculation.

This factor 8/3=2.66667 was tested against the value for 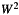$W^2$ , when explicitely derived from a Hanning taper time series by the above formula.

13/9/2007, thof

Implements ts::tapers::Taper.

Definition at line 140 of file tapers.cc.

     {
        const double retval=std::sqrt(3./8.);
        return (retval);
     } // double Hanning::psdnorm() const